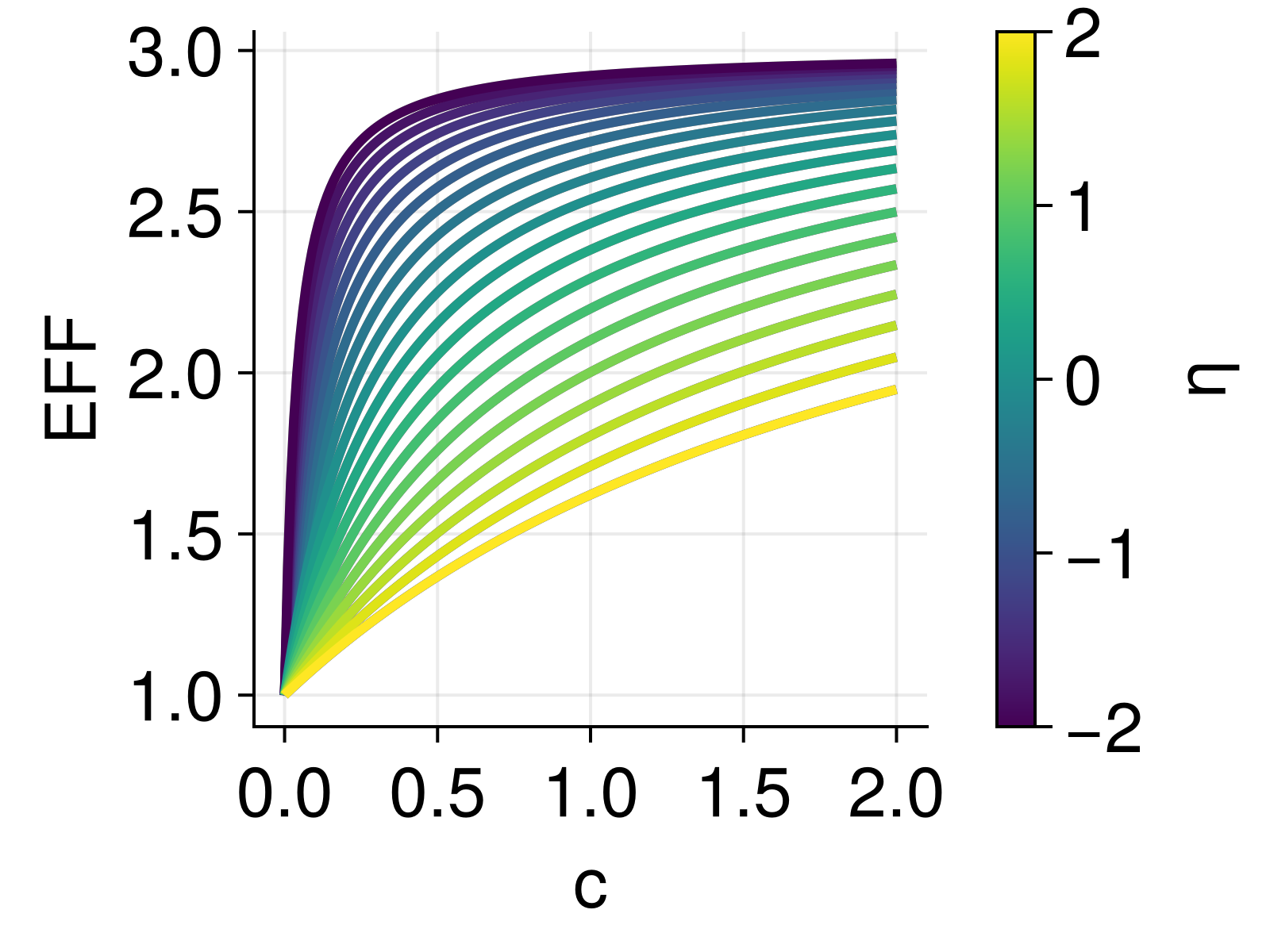Random effects

And how they interact with machine learning

Niklas Korsbo

2025-10-12

Mixed effects (?)

What are mixed effects models?

• Fixed effects, \(θ\)
  • Model parameters modelled as deterministic quantities
• Random effects, \(η_i\)
  • Model parameters modelled as random variables

Hierarchical

We typically define hierarchies where \(θ\) are shared parameters but \(η\) is subject-specific.

No need to assign too much meaning to random effects

• Indicates unknown parameters that vary between subjects (or whatever hierarchy we use)
• Usually tied very closely to a specific parameter in pharmacometrics. \(CL = tvCL \cdot e^{η_{CL}}\)
• Enables degree o freedom along which the model can account for heterogenous outcomes

Simulating with random effects

Simple

• We have given \(θ\) and covariates \(x\)
• Sample from the prior \(η | θ\)
• Compute your individual parameters and propagate your ODE
• Sample your observations \(y | θ, η, x\)

Fitting with random effects

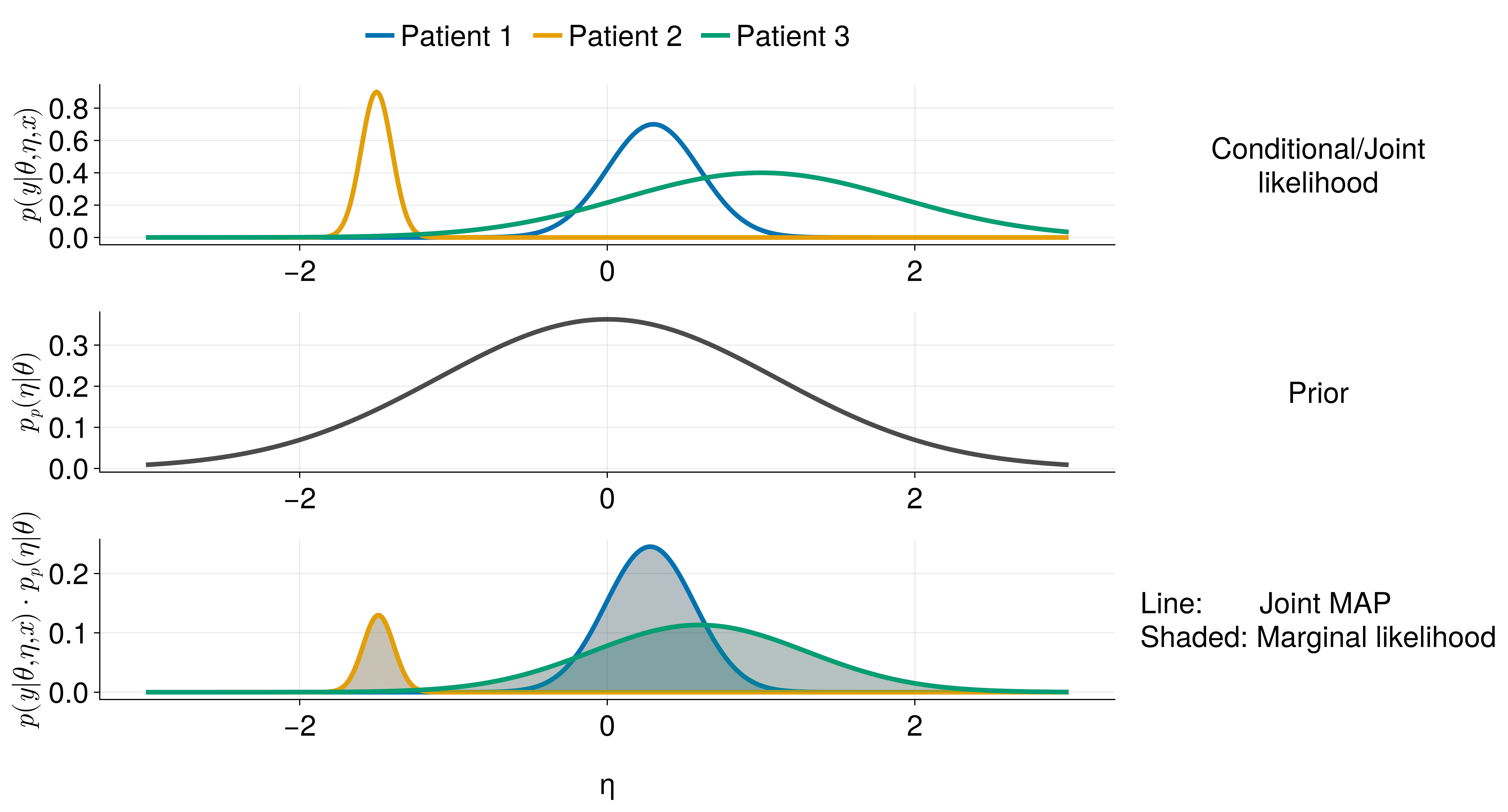
Conditional probability / Joint likelihood / MLE

Probability of the response \(y\) according to the model given specific values of \(θ\), \(η\), and \(x\).

\[ p_c(y | θ, η, x) \]

Fit model by simply finding the values of \(θ\) and \(η\) that jointly maximize the probability?

Equivalent to minimizing a distance metric (e.g. MSE) between observed and predicted data.

Not what we do

Fitting with random effects

Marginal probability

Integrates out the effect of the random effects.

\[ p_m(y | θ, x) = \int p_c(y | θ, η, x) \cdot p_{prior}(η | θ) dη \]

Average conditional probability weighted by a prior

Fitting with random effects

 

One dimension per random effect

• \(η\) here can be multi-dimensional

\[ p_m(y | θ, x) = \int p_c(y | θ, η, x) \cdot p_{prior}(η | θ) dη \]

• This is a multi-variate integral

• One dimension (degree of freedom) along which to account for between subject variability in the data for each random effect.

• Marginalization incentivizes that each random effect controls a single smooth dimension between-subject variability.

“Smoothness”?

Classical NLME \[ EFF = \left(1 + Smax \cdot \frac{C}{tvSC50 \cdot exp\left(\mathbf{\eta}\right) + C}\right) \]

• This function is somewhat smooth in \(η\) by structural definition.
• Very little flexibility to affect the smoothness by tuning fixed effects.

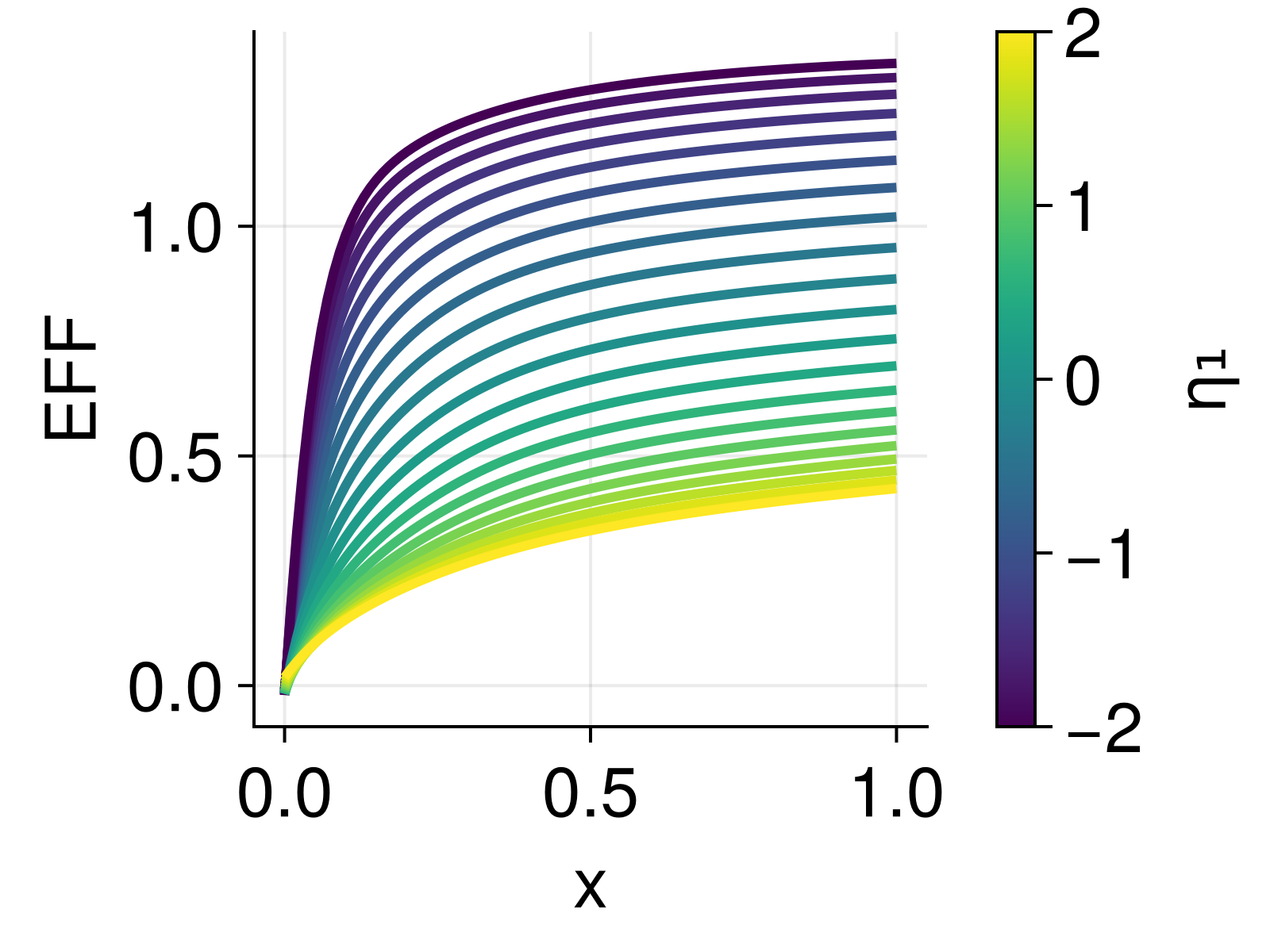
DeepNLME

\[ EFF = \left(1 + NN(C, η)\right) \]

• This function can be very non-smooth in \(η\).
• Lots of flexibility to affect the smoothness by tuning fixed effects.
• Incentivizing smoothness by marginalization in the fit really helps here!

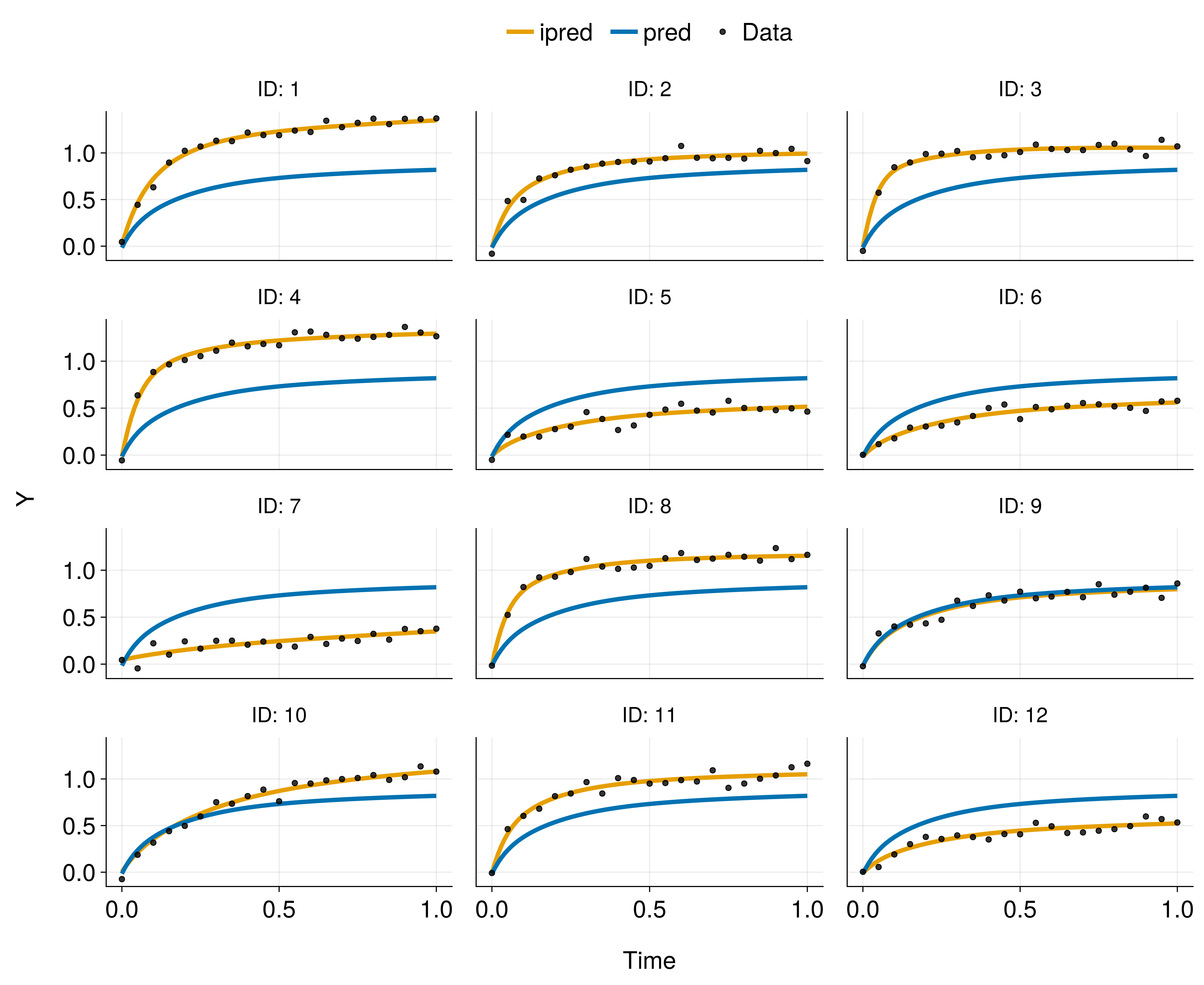
Smoothness in DeepNLME

Data-generating function: \[ Y = \frac{E_{max} \cdot x}{EC_{50} + x} + \epsilon, \quad \epsilon \sim \mathcal{N}(0, \sigma^2) \]

where \[ \begin{align} E_{max} &\sim \mathcal{U}(0.5, 1.5) \\ EC_{50} &\sim \mathrm{LogNormal}(-2, 1.0) \end{align} \]

DeepNLME model: \[ \begin{align} Y &= {\color{orange}NN(x, η₁, η₂)} + \epsilon, \quad \epsilon \sim \mathcal{N}(0, \sigma^2)\\ η &\sim \mathcal{N}(0, I) \end{align} \]

Maximizing the marginal likelihood

The marginal likelihood is often intractable to compute exactly. \[ p_m(y | θ, x) = \int p_c(y | θ, η, x) \cdot p_{prior}(η | θ) dη \]

• No marginalization
  • NaivePooled()
  • JointMAP()
• Maximize an approximation
  • LaplaceI()
  • FOCE() - Often our first choice
  • FO()

• Expectation maximization (EM, indirect)
  • SAEM()
  • Markov Chain EM
  • Variational EM (Later this year)
• Monte Carlo integration
  • BayesMCMC()
  • MarginalMCMC()

Many can be wrapped in MAP() to do maximum a-posteriori estimation of fixed effects.