The Connection Between NLME and Generative AI
Generative AI
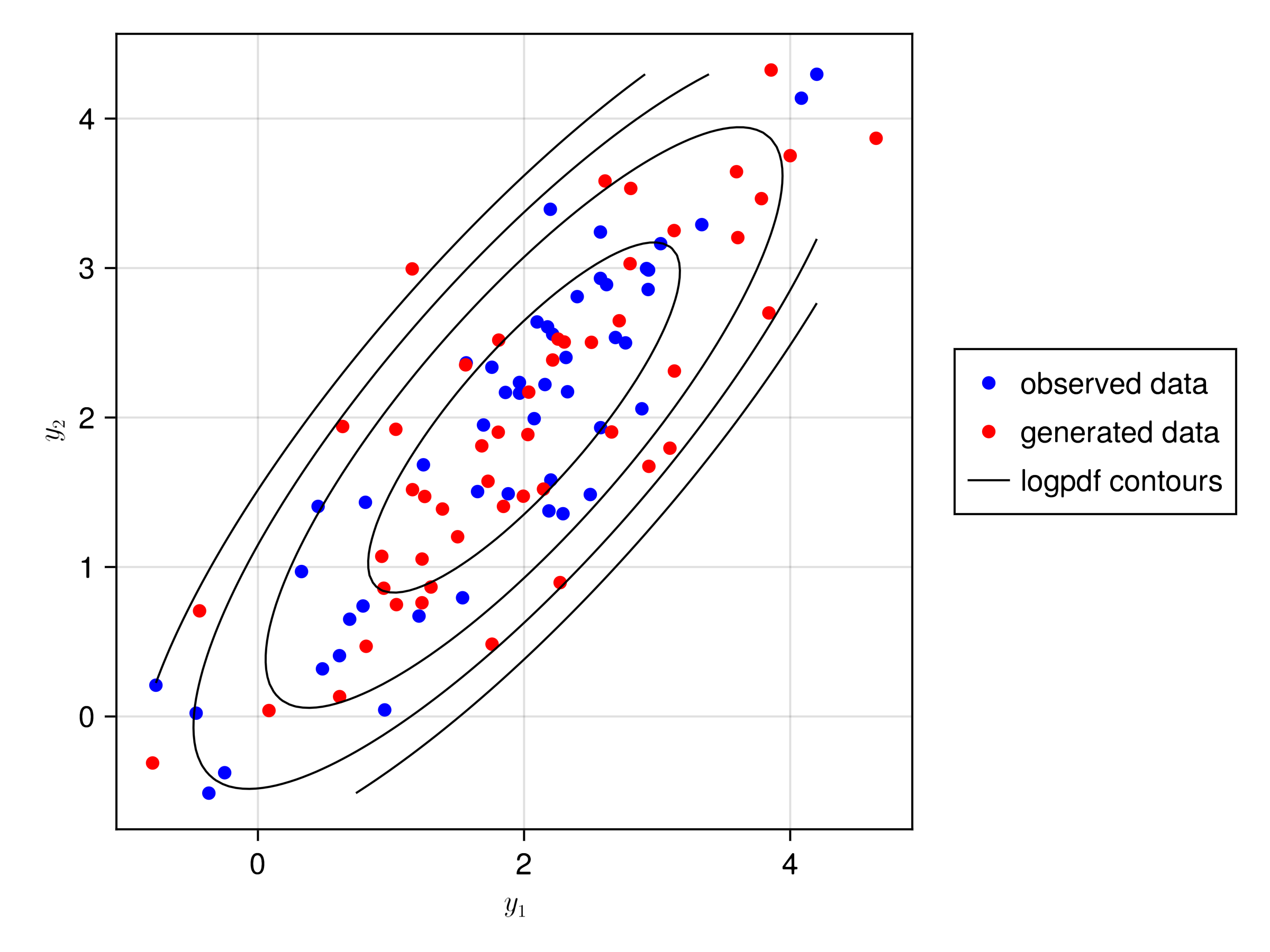
Goal: Generate data indistinguishable in distribution to real data
![]()
![]()
~ ![]()
www.thispersondoesnotexist.com
How is that done?
Data is a mix of
- Observed quantities (pixel intensities)
- Unobserved quantities (faces, smiling, …)
We humans learn to extract the unobserved quantities
GenAI needs to do that too.
How is that done?
Data is a mix of
- Observed quantities (\(y\))
- Unobserved quantities (\(z\) - “latent variables”)
Generative models
- Definitions
- \(z\): latent variables of dimension \(d\)
- \(y\): observed data
- \(y_g\): generated/simulated/synthetic data
- Model
\[
\begin{aligned}
y_g &= f(z) + \epsilon \\
z &\sim Normal(0, I_{d\times d}) \\
\epsilon &\sim Normal(0, \sigma^2)
\end{aligned}
\]
- Objective: find \(f\) such that the distribution of \(y_g\) is close to the distribution of the observed data \(y\)
NLME is Generative AI!
- Definitions
- \(\eta\): latent variables of dimension \(d\) and covariance matrix \(\Omega\)
- \(x\): observed covariates
- \(dv\): observed data/response
- \(dv_g\): generated/simulated/synthetic data
- Model
\[
\begin{aligned}
dv_g &= f_\theta(\eta, x) + \epsilon \\
\eta &\sim Normal(0, \Omega) \\
\epsilon &\sim Normal(0, \sigma^2)
\end{aligned}
\]
- Objective: find \(f\) such that the conditional distribution of \(dv_g | x\) is close to the distribution of the observed data \(dv\)
NLME is Generative AI!
NLME objective: Maximize marginal likelihood of observations \(y\) given covariates \(c\):
\[
p_\theta(y | c) = \int p_\theta(y | \eta, c) \cdot p(\eta) d\eta
\]
Variational Autoencoder (GenAI) objective: Maximize likelihood of data \(x\):
\[
p_\theta(x) = \int p_\theta(x | z) \cdot p(z) dz
\]
They’re identical!
- Random effects \(\eta\) ↔︎ Latent variables \(z\)
- Observations \(y\) ↔︎ Generated data \(x\)
- Individual predictions ↔︎ Generative model
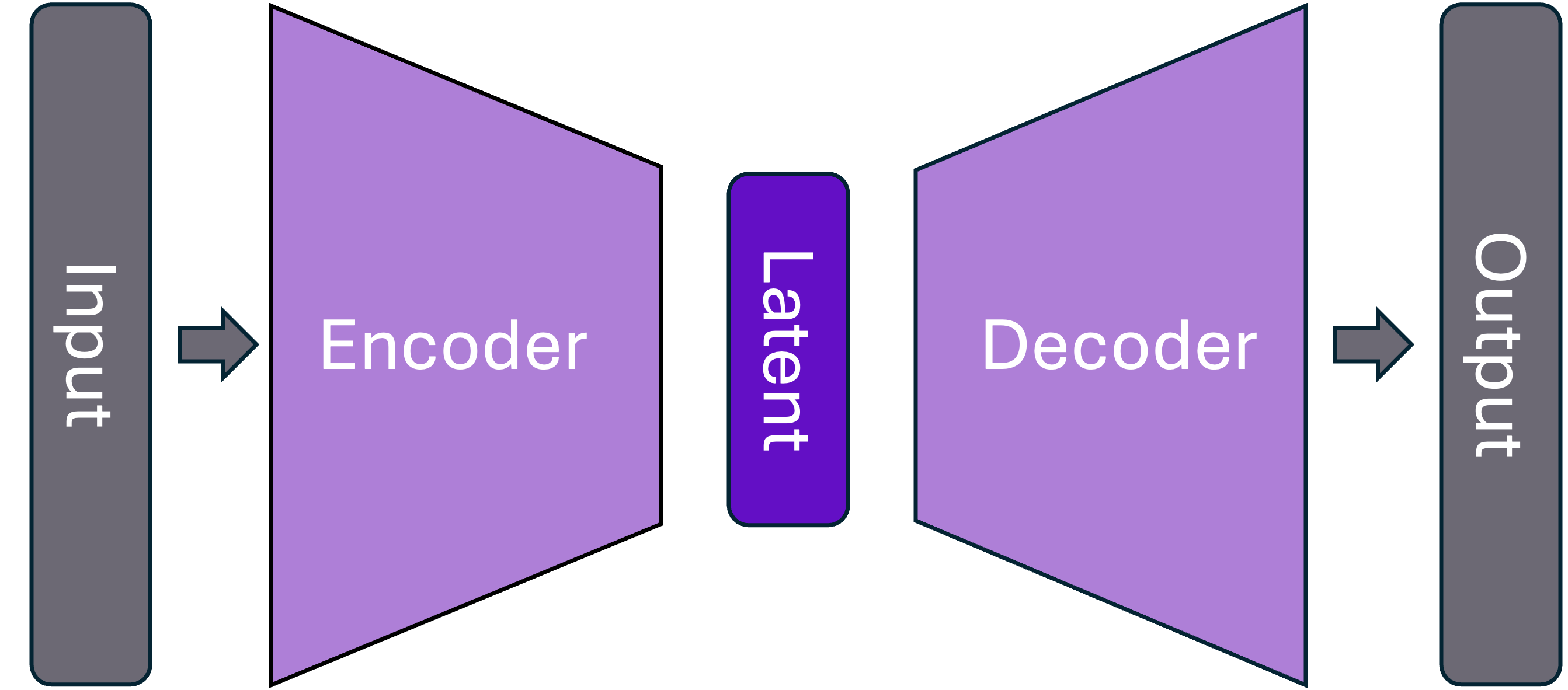
Generative AI – Typical anatomy
![]()
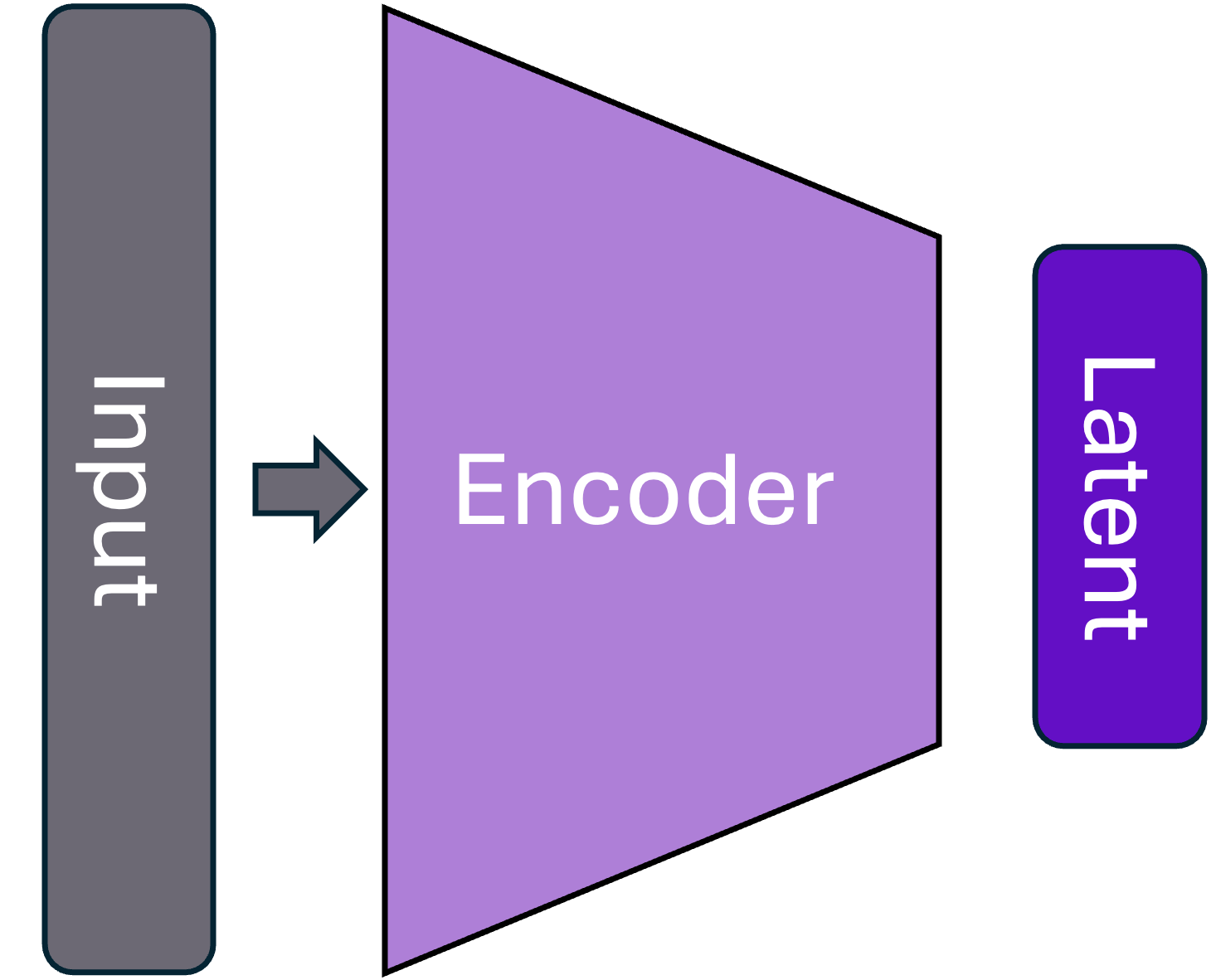
NLME as GenAI
- Input: Time series
- Output: Time series
- Decoder: The “structural” NLME model
- Encoder: an inverse problem of the decoder
What Are Latent Variables?
In Traditional NLME: Meaning is structurally engineered
\[
CL = tvCL \cdot e^{\eta_1}
\]
In DeepNLME: More flexible, but still some structure
\[
\frac{dR}{dt} = NN\left(\frac{Central}{Vc}, R, \eta_1, \eta_2 \right)
\]
In Pure GenAI: Meaning emerges from data and training
\[
p_\theta(x) = \int p_\theta(x | z) \cdot p(z) dz
\]
\(z\) captures informative properties not directly observed
~ 
